Landscape of Debuggability in Machine Learning for Systems
As someone interested in computer systems and machine learning, the intersection of the two fields - machine learning for systems has always fascinated me. My experience during internships at Google Cloud and my discussion with friends at other hyperscalar operators has revealed an interesting pattern: while there’s widespread interest in using machine learning to improve systems, very few ML-assisted systems make it to production. This gap between academic promise and practical deployment raises important questions about the challenges we face in implementing ML solutions at scale.
Academic literature is filled with proof-of-concepts showing ML-assisted systems outperforming traditional methods and heuristics. However, when it comes to actual deployment, the success stories are surprisingly rare. Through an experience paper on ML for systems published by Microsoft and my observations, I’ve found that one of the major challenges in the domain is debuggability - the ability to debug the ML-assisted system when the model misbehaves.
Having made this observation, when I started looking into the academic literature on debuggability, I found it to be quite diffuse. It was scattered across several communities like software engineering, networking, databases, programming languages, and verification. This blog is my attempt at connecting the work done by these communities into an intuitive framework that makes it easier for me to understand and navigate the research landscape of debuggability in ML for systems.
Core Properties
While I’ve talked about debuggability till now, there are three properties at the core of this discussion. Here are the three properties and there definitions :
- Debuggability: the ability to detect and resolve issues that lead to model misbehavior.
- Interpretability: There are two definitions popularized by Molnar’s book:
- Interpretability is the degree to which a human can understand the cause of a decision.
- Interpretability is the degree to which a human can consistently predict the model’s result.
There is a subtle difference between the two - the second definition does not require a causal understanding of the model’s behavior. As long as we can predict its behavior reliably, we say the model is interpretable. This is akin to saying that the phenomena of sun-rise is interpretable by the explanation that the “Sun rises in the east every day” with no actual causal understanding of why the sun rises in the east every day.
The first definition is more strict as it pushes for a causal understanding.
-
Generalizability: model’s ability to perform well on data that is not independent and identically distributed (IID) as the model’s training data.
This is an important property as all ML algorithms rely on the assumption that train and test data are IID. Real world environment frequently violate this assumption due to user behavior pattern changes, workload churn and hardware heterogeneity, and this results in degradation of model performance.
These properties don’t exist in isolation and relate to each other in ways that help one property improve the other. Consider this: ML models inherently have finite generalizability, which means they can struggle with data that doesn’t match their training distribution. This limitation makes model debuggability essential. When debugging the model, we often need to interpretability to understand why the model made certain decisions to find the root cause of the problem. The insights we gain from this interpretation process then feed back into improving the model’s generalizability.
Having defined the core properties, lets move on to the process of debugging. The practice of debugging ML systems involves four essential components:
- Detecting model misbehavior
- Root causing misbehavior by gaining insights
- Correcting model misbehavior
- Preventing model misbehavior
Detecting Model Misbehavior
The two interesting questions in this subspace are
- How to detect model misbehavior?
- When to detect model misbehavior?
The answer to the first question depends on the answer to the second question. Hence, I will taxonomize the discussion based on potential answers to the second question.
One can detect model misbehavior:
- Reactively : once the model is deployed and performed inference to generate prediction
- Proactively after Deployment : once the model is deployed but before/along with the model’s inference.
- Proactively before Deployment : before the model is deployed, but after it has been trained and validated.
Reactive Misbehavior Detection
Here, if we have the ground truth available, we can compare predictions with ground truth - for instance, comparing predicted versus actual latencies in power management systems like ReTail. In cases where ground truth isn’t readily available, like in autoscaling systems when model output is number of service replicas, we can monitor target metrics such as SLO violations to identify potential issues with model behavior.
Proactive Misbehavior Detection
Proactive detection takes a more preventive approach and can occur at two crucial stages. During deployment we can run uncertainty estimators during/before model’s inference to measure the model’s confidence in its predictions, as shown in Figure below.

These estimators can be as simple as distance measurements or can be more complex like density estimation tools or Bayesian neural networks that output probability distributions rather than point estimates. When uncertainty levels are too high, one can choose to ignore the model’s predictions entirely.
We can also diagnose model misbehavior before deployment! There are two major approaches proposed here:
- Data slicing
- Model verification
Data Slicing
The goal of data slicing is to identify subsets of data (”slices”) where the model might misbehave. A slice is defined as a conjunction of feature-value pairs and the process of slice identification is run on a held-out validation dataset. A problematic slice is identified based on testing of a significant difference of model performance metrics (e.g.,loss function) of the slice and its counterpart. As datasets have grown larger, this process has been automated. The common approached for slice identification are:
- Clustering: This approach involves grouping similar examples together and treating each cluster as a data slice. If a model underperforms on any of the slices, the user can analyze the examples within that cluster. However, this approach has drawbacks, such as difficulty interpreting high-dimensional data and the need to specify the number of clusters.
- Decision Tree Training: This method trains a decision tree to classify which slices are problematic. The leaves of the decision tree correspond to slices. While this offers a natural interpretation, it may not find all problematic slices, as it only searches non-overlapping slices.
- Lattice Searching: This approach considers a larger search space where slices can overlap. It traverses a lattice of slices in a breadth-first manner, checking for effect size and statistical significance. This method can be more expensive but provides a more comprehensive search. **
Relevant papers: Automated Data Slicing, Explaining Mispredictions
Model Verification
Verification is a way to guarantee that the model meets a user-specified requirement or alternatively, for identifying a scenario or counterexample where the requirement is violated. This generation of counter-examples helps identify and detect model misbehavior before deployment.
This definitely necessitates that users are able to formally specify their requirements or properties as specifications understood by the verifier.
The most common types of properties are:
- safety: guarantees that nothing bad happens
- liveness: guarantees that something good happens eventually
- monotonicity: output decreases/increases in line with input in a monotonic fashion
Next, the model and system is encoded in a graph representing states and the corresponding transitions. Once this encoding is done, the specified properties can be checked by verifier using techniques like bounded model checking, k-inductions and invariant inference.
The major issue with verification is poor scalability. However, prior works have shown that verification is still useful for models deployed for systems tasks as:
- The models used for systems tasks are small
- The input features are highly engineered which allows expression of complex system properties
For a more detailed discussion on neural network verification for systems, please refer to Appendix. Yes, I geeked out and wrote an appendix for a blog post!
Root causing misbehavior by gaining insights
This is where interpretability of model plays a key role. To reiterate the purpose of interpretability is to gain insight to explain the model’s decision making process. However, it is not clear what is a good explanation and what insights help in explaining the model’s decision making process. I briefly talk about some work on formalizing the notion of a good explanation at the end of this section.
The insights one aims to gain from interpreting the model depend on one’s definition of interpretability. If one follows the second definition of interpretability given previously, then one is only interested in identifying patterns in model’s decisions which make the model’s decision-making predictable. Here, one is only interested in answering the question “When does a ML model misbehave?”. On the other hand if one follows the first definition of interpretability given previously, then one is interested in answering “Why does a ML model misbehave?”.
When does a ML model misbehave?
Here, the idea to discover patterns to find when the model is predictably wrong. This usually translates to identifying data samples on which the model misbehaves. Data slicing is the approach used for identifying subsets of data on which the model has low performance. These data subsets or slices are identifies using a decision list - a conjunction of feature-value pairs. These slices are considered interpretable when the length of decision list is small i.e they only have a handful of feature-value pairs.
Why does a ML model misbehave?
The aim of this question is to uncover the causal structure of the model’s decision making process. This is an ambitious goal where people have only seen partial success. Below are some methods that researchers have proposed:
Building surrogate models
The idea is to train a inherently interpretable model (surrogate) that mimics the original complex model. Surrogates are trained using some form of teacher-student training.
Since the surrogate is inherently interpretable like a decision tree or spare linear model, one can easily extract the model’s decision making process from it. While this seems great , this approach has the underlsing assumption that since the decisions made by the surrogate mimic that of the original model, the decision-making process of the surrogate also mimics that of the original model. This assumption is not necessarily true. Even if that assumption holds, since the surrogates have low complexity, it is usually not possible to capture the entire decision-making process of the complex original model in the surrogate. This results in surrogates having lower performance than the original model and exposes a complexity-performance tradeoff.
Relevant Papers: Interpreting DL-based Networking Systems, PRIMO
Counterfactuals
Counterfactuals help us answer “what-if” questions. For example, what would be the predicted latency if the cpu utilization was 2X instead of X? Usually, the explanations here provide data examples where the model’s prediction changes significantly on a minor pertubation to the input or an input feature. Usually counterfactuals are implemented using causal inference where the system is modeled usng Bayesian Networks or Structural Causal Models (SCM).
The disadvantage of this approach is that for each input sample one can generate multiple counterfactual explanations. Some of this counterfactual explanations might be inconsistent with each other. Hence, it is difficult to figure out which counterfactual explanations to use.
Relevant Papers: Counterfactual Explanations for Models of Code
Feature attributions
The idea here is to assign an importance score to each feature in the input or provide a relative ranking of feature importances. The intuition being that the model misbehavior can be explained most by the feature having the largest contribution/importance in producing the model’s output. Multiple techniques like LIME, Shapely values, SHAP can be used to get this feature importances. For more complex networks like LSTMs or transformers, attention values are used to obtain feature importance. and many time simple techniques can lead to important insights. For example in SINAN, authors were able to identify a faulty configuration of redis using LIME to interpret their CNN model.
These approaches provide useful insight into which features are the most relevant and can act as good starting points in the debugging process. However, their disadvantage is that they do not provide any understanding of what the model is learning and how the features interact together to produce the final prediction. Hence, it has minimal contribution to out understanding of the causal structure of the model’s decision making process.
Relevant Papers: SINAN, Applying Deep Learning To The Cache Replacement Problem
Data attributions
The general idea behind data attribution is to identify the training data samples that contributed most to the model misbehavior. The assumption here is that the set of training samples contributing most to model behavior can be easily grouped together to represent a human-understandable concept.
It is easy to confuse data attribution with data slicing, however, there is a subtle difference. Data slicing seeks to identify data subsets on which the model misbehaves. On the other hand, data attribution seeks to identify training samples which contribute most towards model (mis)behavior. So for a model behavior, data attribution provides the training examples which contributed the most positively and negatively to the model behavior. The difference is that data attribution tries to distinguishes between the training sample on which the model misbehaves and seeks to give them a contribution score.
My friends at MIT organized a great tutorial on Data Attribution at ICML 2024. To learn more, please refer to their tutorial.
Neuron attributions
The idea here is attribute the model misbehavior to a given fault neuron or a group of neurons in the model. As we are talking about neurons, this approach is targeted towards neural network interpretation.
MODE identifies the neurons causing misbehavior using a two-step process - first it identifies the layer and next it identifies the neuron within the layer.
For doing so it selects a layer, it freezes the network upto the selected layer and adds a new output later (shown in figure below). Then it trains just the output layer again. It repeats the procedure for all hidden layers in the network. It selects the first hidden layer for which the model’s accuracy it higher or equal to the original model’s accuracy. The intuition is that the features represented by the selected layer are good enough to perform the prediction and later layers are not essential . Finally, to select the neuron within the selected layer, the authors analyze the weights between the selcted layer and the new output layer. Higher weight magniutde signifies higher importance.
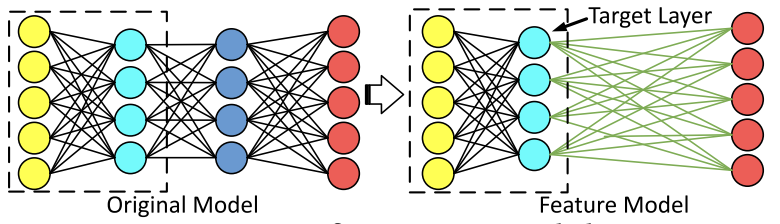
The machine learning community has also directed its efforts towards “mechanistic interpretability” - a field aimed at reverse-engineering the model. Initial efforts have shown that neurons/neuron groups within a model can be mapped to human-understandable concepts and algorithms learned by model to combine the different concepts together to form the output. Future efforts in this direction by systems researchers can help reveal the underlying algorithm learned by the model and help us move forward from current attribution-based appraoches.
Notions of a good explanation
It is surprisingly difficult to define a good explanation.
Christopher Molnar says that a good explanation has the following properties - accuracy, fidelity, consistency, stability, comphrehensibility, certainty degree of importance, novelty and representativeness. For definition of the properties refer to the Interpretable Machine Learning book.
Jia et. al. have formalized the notion of a “sound explanation” by restricting it to four properties- specificity, additivity, completeness, and baseline invariance.
Here are the definitions of these properties (copied from the paper):
- Specificity: An interpretation should be specific to influential inputs: it should assign zero scores to inputs that do not influence function values.
- Additivity An interpretation is additive if its attribution decomposes over function addition.
- Completeness An interpretation is complete if its attribution explains all of the output.
- Baseline invariance A baseline-invariant interpretation generates the same rank of inputs for different choices of baseline input.
While this formalization might seem arbitrary, the paper discusses good logical arguments for including each property. More importantly, it leads to a crucial theorem : No attribution algorithm can satisfy all 4 four of the aforementioned properties at once. This discourages the practice of interpreting models by assigning attribution scores to input components.
Correcting model misbehavior
Model’s parameters dictate the model’s behavior. Hence, correcting the model’s behavior translates to modifying the model’s parameters. The widely adopted way of modify model’s parameters is to use a training algorithm like gradient descent. However, if one knows the neuron-level attributions for a neural network one can also manually adjust the parameter of the neuron to change model’s behavior
Retraining
The most obvious way to correct mode behavior is to retrain the model on a dataset which has examples on which the model misbehaves. Machine learning models deployed in production are usually trained periodically on all collected data to handle issues of distribution drifts (poor generalization).
Unfortunately, training is a time-consuming, resource intense and costly process. Hence, any efforts to optimize the training process are useful.
There seem to be two questions that are important to answer when optimizing retraining:
- When to retrain the model?
- On what data to retrain the model?
When to retrain the model?
We want to retrain the model only when needed. That is to say, when the we see a distribution shift in the input data (data distribution is OOD) and the benefit of retraining out weights its overhead.
It is easy to estimate the overhead of retraining since one knows it from past experience. However, is non-trivial to estimate the benefit of retraining the model. Instead one can approximate benefit of retraining by using the uncertainty of model’s predictions averaged over recent predictions. One can also use Out-Of-Distribution (OOD) detection methods to detect a distribution shift and trigger retraining based on this detector.
Relevant paper: DecTrain
On what data to retrain the model?
The retraining dataset should obviously include examples of data on which the model misbehaves. The dataset should also include examples where the model already behaves well. Examples of both types (where model misbehaves and where model behaves well) are essential to avoid dataset imbalance issues.
What is not obvious is how many of each type of examples should be in the retraining dataset and which examples of each type should be included.
To answer these questions, data attribution methods can be useful. Data attribution tells us which examples in the training set had the most positive/negative contribution to the model’s behavior. Hence, when creating a dataset for treating model misbehavior one should include:
- deployment-time examples on which model misbehaved
- training set examples which had most negative contribution to model misbehavior.
- training set examples which had the most positive contribution to desired model behavior.
To decide how many examples to include, once can decide a threshold attribution value and include examples above that threshold.
Currently, data attribution methods work well on strongly convex models, however this is a growing field and I hope we will soon have efficient predictive attribution estimators for deep neural networks as well.
Model Surgery
If one uses neuron-level attribution methods to interpret the model, one can map a subset of model or a neuron to a human-understandable concept. If this is possible, then one can potentially just change the weight (parameter) associated with that neuron to change model behavior when dealing with the corresponding concept.
This has been shown to work well on non-systems based ML models. Famous examples are the ROME paper and the Golden-Gate Claude. The former identifies neurons with an LLM that store the fact that “Colosseum is in ROME” while the latter identifies neurons in Claude corresponding to the Golden Gate Bridge. By modifying the neurons, the researchers show that they can change fact learned by the model - that is the model will now store the fact that “Colosseum is in Paris” or can force to model to focus on the concept even when not required; in case of Golden Gate bridge Claude, the LLM would inevitably try to include something about the golden gate bridge in its responses.
While there has not been MLSys work on model surgery I believe that this would be greatly beneficial in the field and eliminate a large portion of debugging overhead.
One underlying assumption with this approach is that individual neurons map to single concept. That is changing the neuron value to improve model behavior on one concept does not degrade its behavior on another concept.
Preventing model misbehavior
Much like healthcare, prevention is better than cure in MLSys as well.
Below are a few ways to prevent model misbehavior:
Add guard rails
The simples way to prevent known errors is to limit the model output by adding some guard rails. This guard rails could be in form of output clipping or threshold checking. While very simple to implement it woks only for known issues with the model and most likely will fail on unknown issues.
Use predictability of model misbehavior
As discussed previously, there have been proposals to add an uncertainty estimator to systems to estimate the model’s confidence in it prediction. When the uncertainty is high, the system may choose to ignore the model’s prediction and fall back to a well-studies heuristic method. Further, the same strategy can be used when we have identified data subsets on which model misbehaves using data slicing before deployment.
In reinforcement learning settings, similar proposals are popular under the name of “online safety assurance”. At a high level these proposals, fall back to a well-studies heuristic policy when the RL system reaches an “unsafe” region during its exploration phase.
Use a model ensemble
Here the idea is to use an ensemble of “expert” models and dynamically select the best model from the ensemble for prediction for each input sample. Most of the research focus here seems to be on model selection algorithms.
The trivial selection algorithm would be to run all models and then report some aggregate metric of all model outputs. However this is resource intensive. Alternative proposals use a neural network to select which model(s) to use for prediction. RECL use a gating network which assigns a score to each model in the ensemble. Models with score higher than a threshold are used for prediction. Ivy use meta-learning to learn a model selection policy and uses that to select a single model that is used for prediction.
Change model structure
Model structure provides an “inductive bias” which can help the model learn better on particular domains.
The most successful examples here encode the causal relationships between the observable and latent variables as a Bayesian Network. The benefit is not only that the model knows the causal relationships but also that now we can learn the distribution of latent confounders.
Onelearn the conditional probabilities between variables using vanilla machine learning. Finally, performing causal inference on this new structure allows them to generate accurate counterfactuals.
The downside of this approach is that sometimes the causal relationships are not obvious or too difficult to capture. Further, a fundamental research question in causality is how does one know the number of latent confounders? Hence, researchers using this need to guess the number of latent confounders and hope that their guess leads to a decent approximation of the actual latent confounders.
Relevant Papers: SAGE, CausalSim
A recent work OSPrey, has shown that separating the model into multiple parts - one for learning system context, one for learning workload characteristics and one for cobining the previosu two parts, can be beneficial for generalization.
Change learning algorithm
The reinforcement learning community has designed several learning algorithms, few of which have shown to improve generalization of learned policies. One such algorithm is curriculum learning.
In curriculum learning the training environment distribution is changed to gradually increase the difficulty of training environments or decreasing order of rewardingness. The challenge in applying this training algorithm to MLSys is that we do not have a clear way to measuring the difficulty or rewardingness of a training environment.
GENET proposes gap-to-baseline as a difficulty measure - how much the RL policy’s performance falls behind a traditional rule-based baseline. If environment has large gap-to-baseline, since the baseline already shows how to perform better in the environment, the RL model may learn to “imitate” the baseline’s known rules while training in the same environment, bringing it on par with—if not better than—the baseline. On the flip side, if an environment has a small or even negative gap-to-baseline, chances are that the environment is intrinsically hard (a possible reason why the rule-based baseline performs badly), or the current RL policy already performs well and thus training on it is unlikely to improve performance by a large margin. GENET applies this algorithm to networking problems like adaptive bit rate selection and congestion control.
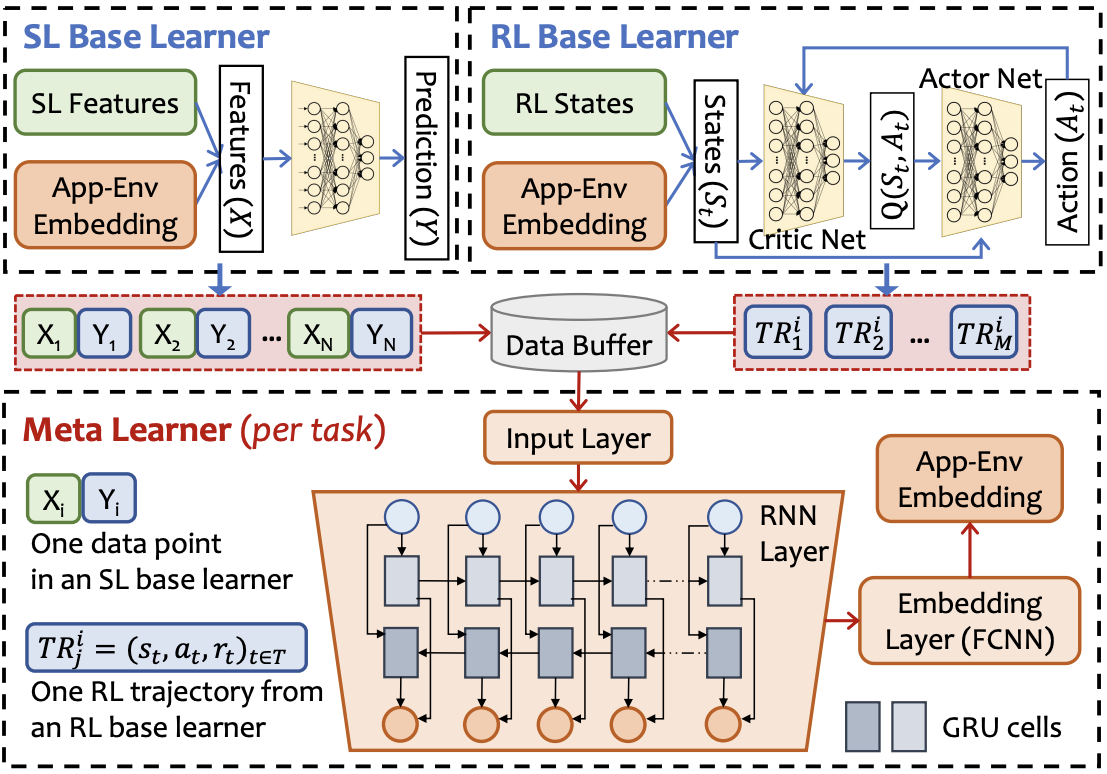
Another proposal is FLASH, which learns a app-environment embedding and uses it for downstream tasks like schedule and autoscaling. To adapt to distribution shifts, it uses metalearning to constant modify the app-environment embedding generator. The high-level diagram is below:
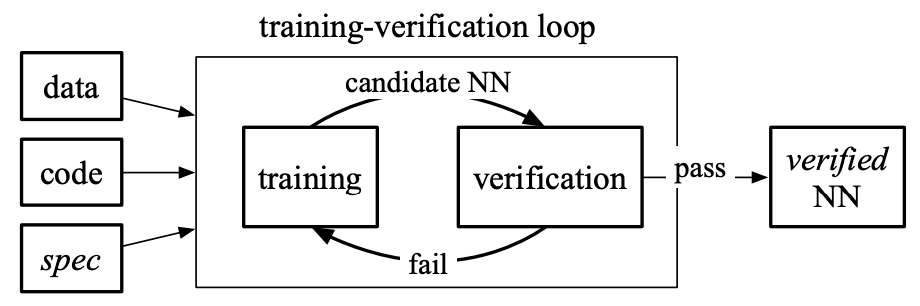
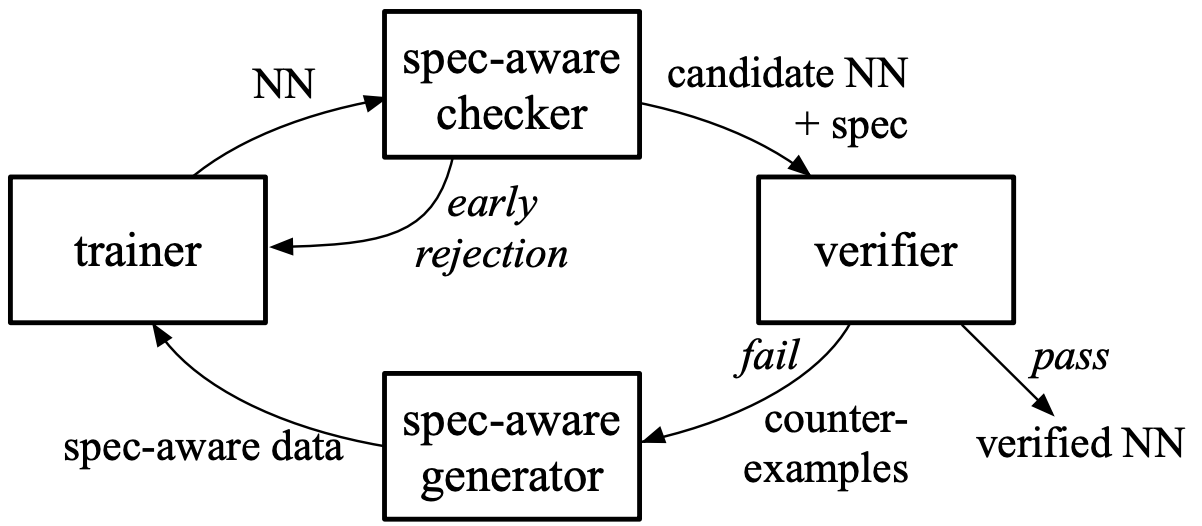
An alternate propsal, Ourboros, proposes including the verifier in the training pipeline to ensure that the trained networks follow the provided specifications. Figures below show the high-level block diagrams of such verifier-in-the-loop training processes.
Appendix
Neural Network for Systems (NN4Sys) Verification
Relevant papers and Sources:
- Verifying learning-augmented systems
- Towards Scalable Verification of Deep Reinforcement Learning
- AutoSpec: Automated Generation of Neural Network Specifications
- Specification Generation for Neural Networks in Systems
- NN4SysBench: Characterizing Neural Network Verification for Computer Systems
- Building Verified Neural Networks for Computer Systems with Ouroboros
Neural networks for systems are attractive candidate for verification. These networks have well-engineered features which allows for smaller network sizes and ease in specifying complex relationships between features. These properties help mitigate the scalability bottlenecks of neural network verification.
A neural network verification query has 3 parts:
- neural network N
- input property P
- output property Q
A DNN verifier answers the question,
“Does there exist some input x, such that P(x) is True and Q(N(x)) is also True?”
N(x) represents the output vector of the neural network
Verifier can produce two types of outputs:
- UNSAT, meaning no such input exists
- SAT, with a concrete example satisfying input
The properties to verify - P and Q are also called specifications.
There are multiple formal verification techniques to use this verifier for verifying the specification. Prior work on verifying neural networks used for systems tasks has used (bounded) model checking, k-induction and invariant inference.
When using model checking, the system needs to be formalized as a state machine - with a initial state, a set of all possible states, a transition function, and some predicates/functions for classifying a state as good or bad.
When verifying deep reinforcement learning policies, the states in this state machine correspond to the inputs of the neural network - which could be the environment state or the history of environment states. The transition function is usually over-approximated i.e. for transition function T, if T(x, y) is False then y is not reachable from x, however if T(x, y) is True, then y might not be reachable from x. The reason for over-approximation is to avoid complexity when defining the transition function. Finally, the one can have a single predicate to classify a state as good/bad, or one can have two separate predicates G and B for classifying states as good and bad respectively.
Having encoded the system into a state machine, the next step is to come up with properties to verify or specifications. In systems, useful properties/specifications discovered till now, fall into the following categories:
- safety: guarantees that nothing bad happens
- liveness : guarantees that something good happens eventually
- monotonicity: output decreases/increases in line with input in a monotonic fashion
- probabilistic: the neural network follows a rule with some given probability
Usually, when defining Q, we define it to be the negation of our desired property. Hence, if the verifier returns UNSAT, then the property holds. However, if the verifier returns SAT, then the property does not hold.
Usually, the properties or specifications are manually written. However, it is difficult to write comprehensive set of specifications for large systems. Hence, researchers have also proposed generating the specifications from data - using techniques like grid-search, clustering and decision tree traversals.
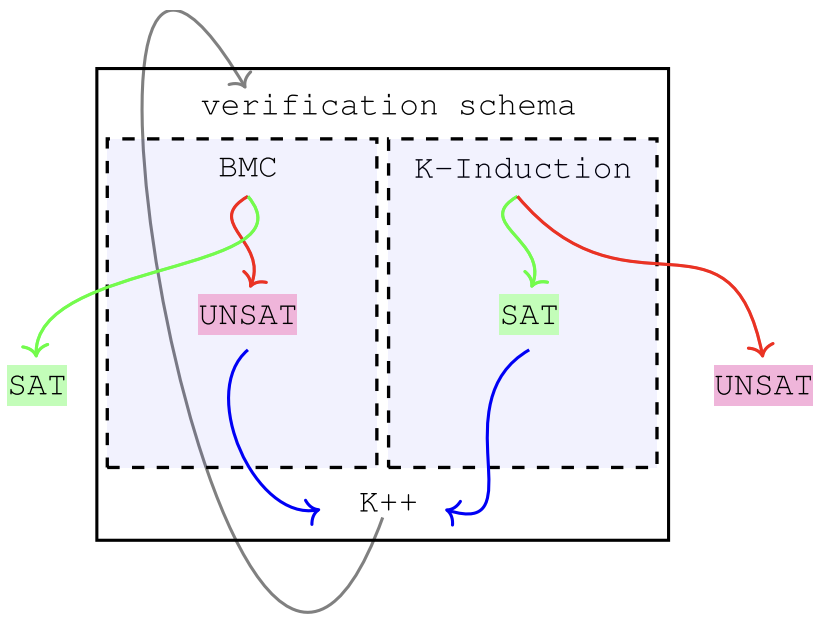
Finally, since a particular execution of the systems can have a huge number of state transitions, we need to bound the the number of state transitions we consider in a given execution to improve the scalability of the verification approach. Hence, instead of model checking, we actually perform bounded model checking and also specify the number of transitions/steps (k) that will be considered. When using bounded model checking, one first runs the verifier with a smaller value of k, if the verifier returns SAT then you know for sure that the property does not hold. However, if the verifier returns UNSAT, then we cannot surely say that the property holds and need to try higher values of k. Hence, bounded model checking is useful for refuting a property but cannot be used for proving a property.
To prove a property, one can use a verification technique called k-induction. The idea here is to find execution sequences with length of k steps, which can start from any state and for which the property is False. If the property is False, we will find a sequence of length k and we should also be able be find a sequence of length k+1 that violate the property. However, if we find a sequence of length k that violates the property but cannot find a sequence of length k+1 , then the violating sequences of length k are not reachable from the initial states. Hence, the property must be True.
Hence, if a verifier finds that a k-induction query is UNSAT, we know that the corresponding property holds. However, if it returns SAT with a counter-example that does not start at an initial state, we cannot conclude whether the property holds, and must increase the value of k.
Whirl 2 proposal combines bounded model checking and k-induction as shown in figure below to either prove or refute a property/specification.
Next, I’ll define invariant inference.
An invariant is a partition of the state space into two disjoint sets such that the two sets are disconnected. Such invariants are useful when all initial states are in one set and all bad states are in the other set. This invariant would show that none of the bad states are reachable.
Finding such invariants turns out to be undecideable in the general settings and hence the prior work proposes using semi-automated invariance inference. They use the observation that the systems of interest tend to behave like Boolean monotonic functions, they are satisfiable when the input range is large, but become unsatisfiable when input range is narrowed. Finding the tipping point in useful to proving properties.
These verification approaches do have there fair share of limitations:
- Poor scalability with network size (exponential). This is further exacerbated when verifying RL policy networks as one has to duplicate the network multiple times, once for each RL step.
- Current verifiers work only for feedforward neural networks with piece-wise linear activation functions.
- Current verifiers do not support monotonic specifications.